二木的博客

Appearance

Return to top
目录

二叉树

满足每个节点度不大于2，孩子节点次序确定的树

特点

  1. 每个节点最多有两颗子树，所以二叉树中不存在度大于2的节点。
  2. 左子树和右子树是有顺序的，次序不能任意颠倒。
  3. 即使树中某节点只有一棵子树，也要区分它是左子树还是右子树

性质

  1. 在二叉树的第i层上最多有2^(i-1) 个节点 。（i>=1）
  2. 二叉树中如果深度为k,那么最多有2^k-1个节点。(k>=1）
  3. n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。
  4. 在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。
  5. 若对含 n 个节点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的节点有如下特性：
    1. 若 i=1，则该节点是二叉树的根，无双亲, 否则，编号为 [i/2] 的节点为其双亲节点;
    2. 若 2i>n，则该节点无左孩子， 否则，编号为 2i 的节点为其左孩子节点；
    3. 若 2i+1>n，则该节点无右孩子节点， 否则，编号为2i+1 的节点为其右孩子节点。

分类

满二叉树

如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

满二叉树

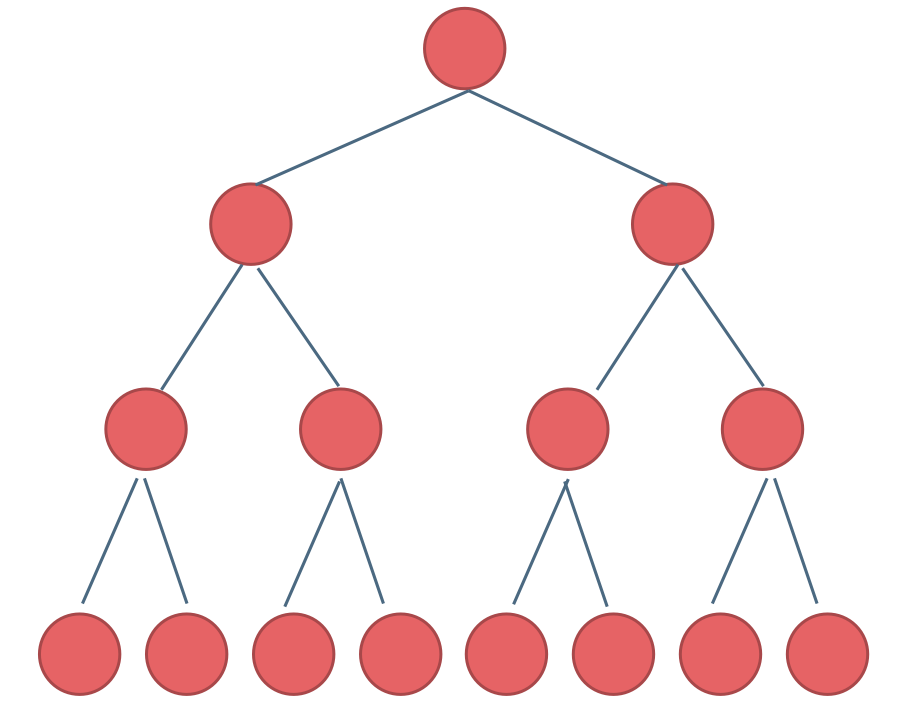
这棵二叉树为满二叉树，也可以说深度为k，有2^k-1个节点的二叉树。

完全二叉树

在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。

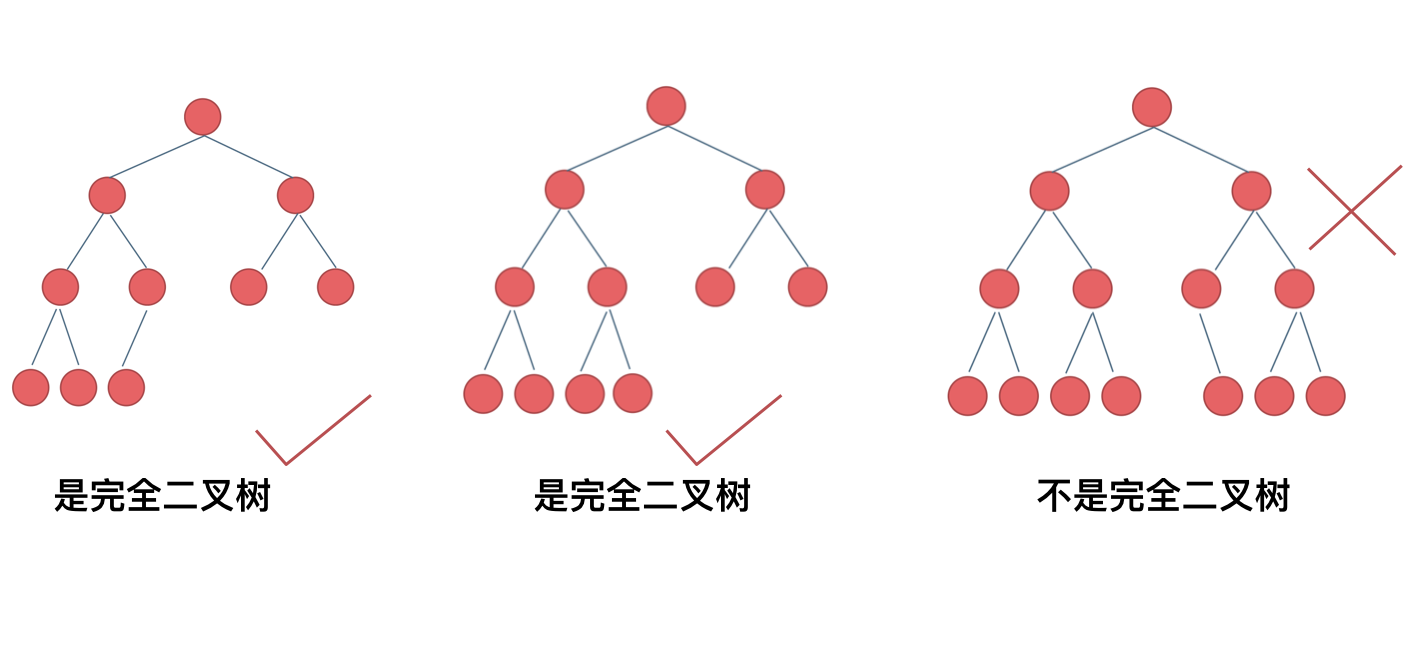
完全二叉树

二叉搜索树

二叉搜索树是有数值的，二叉搜索树是一个有序树。

  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  • 它的左、右子树也分别为二叉排序树

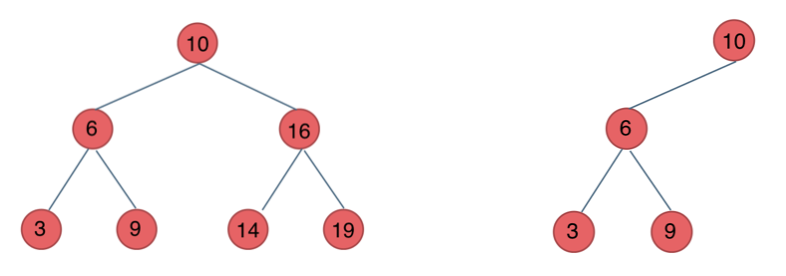
二叉搜索树

平衡二叉搜索树

又被称为AVL（Adelson-Velsky and Landis）树 ，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

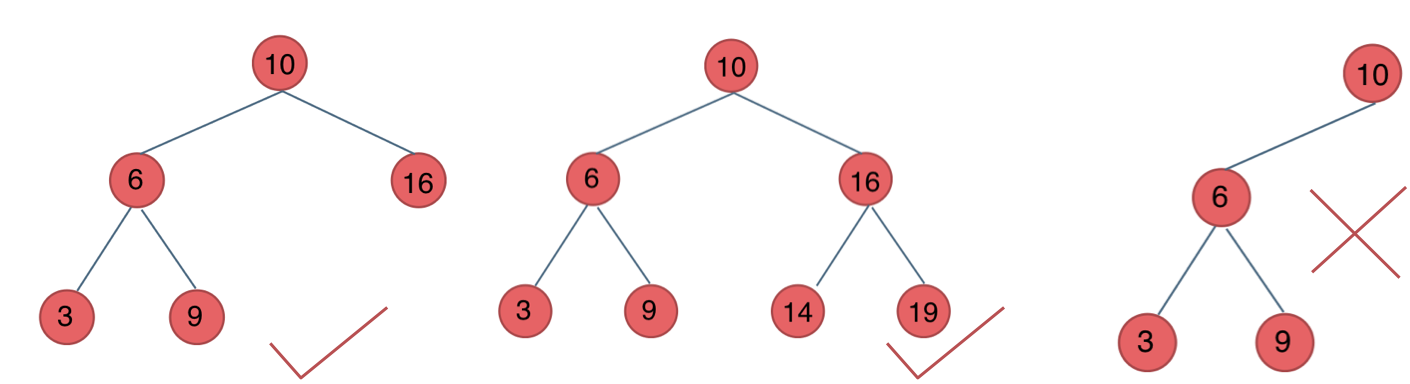
平衡二叉搜索树

存储方式

二叉树可以链式存储，也可以顺序存储。

链式存储如图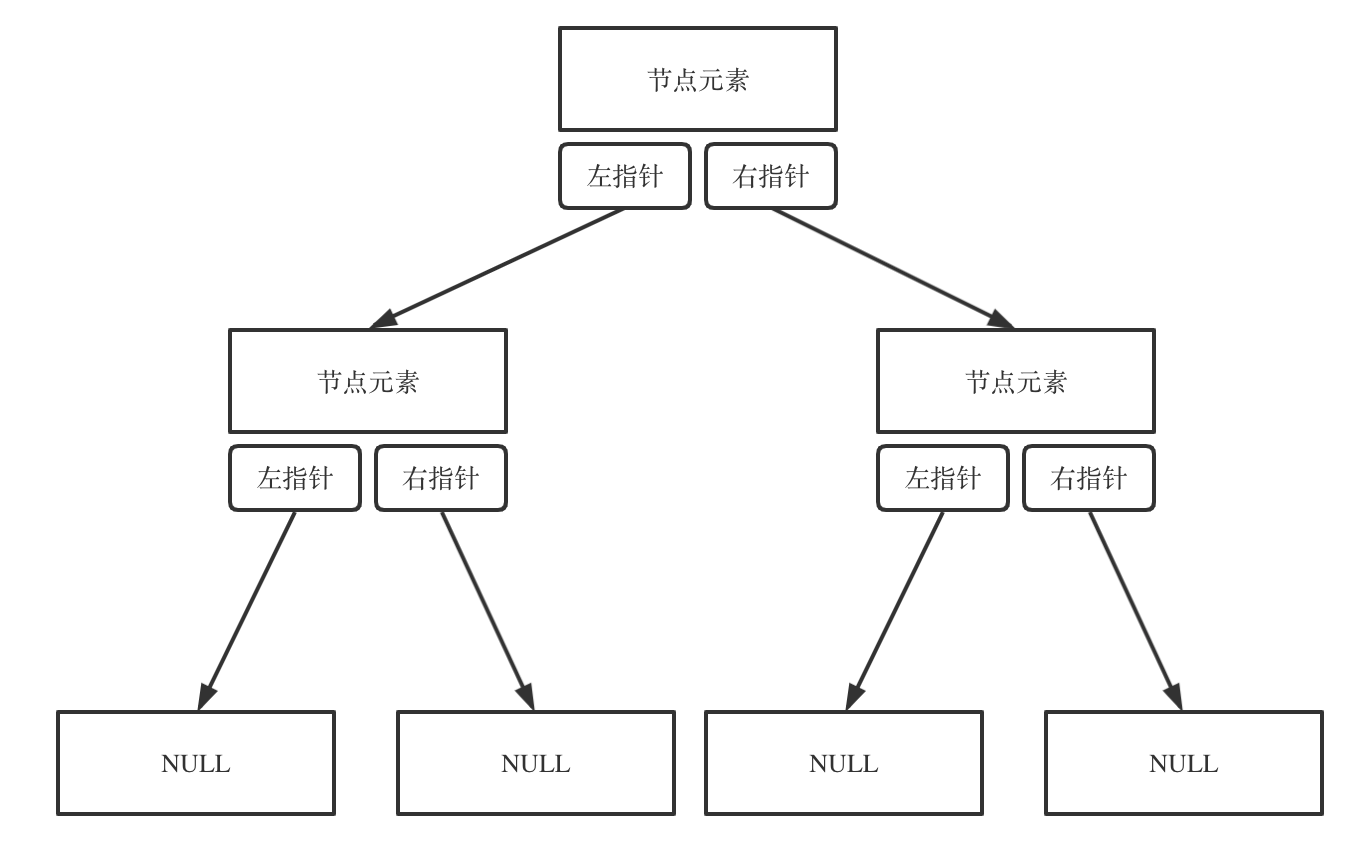： 链式存储

顺序存储的方式如图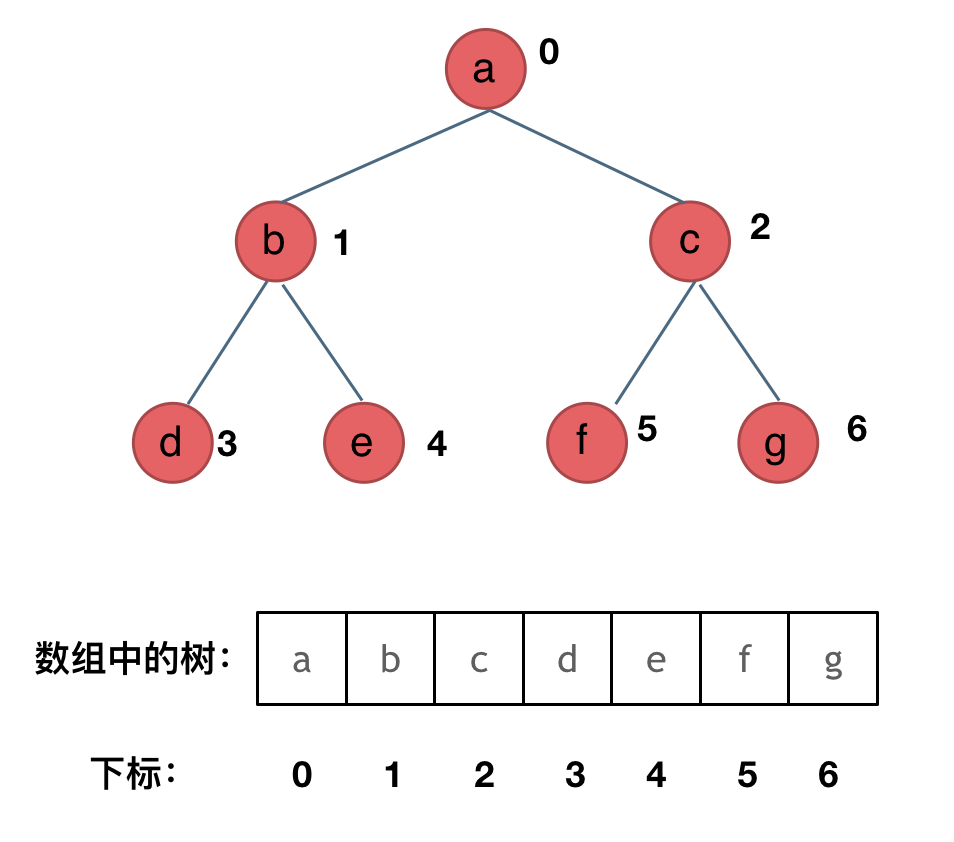： 顺序存储 如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

遍历方式

二叉树主要有两种遍历方式：

  1. 深度优先遍历：先往深走，遇到叶子节点再往回走。
  2. 广度优先遍历：一层一层的去遍历。

那么从深度优先遍历和广度优先遍历进一步拓展，才有如下遍历方式：

  • 深度优先遍历
    • 前序遍历（递归法，迭代法）
    • 中序遍历（递归法，迭代法）
    • 后序遍历（递归法，迭代法）
  • 广度优先遍历
    • 层次遍历（迭代法）

在深度优先遍历中：有三个顺序，前中后序遍历，这里前中后，其实指的就是中间节点的遍历顺序。

递归遍历

递归三要素

  1. 确定递归函数的参数和返回值：确定哪些参数是递归的过程中需要处理的，那么就在递归函数里加上这个参数， 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
  2. 确定终止条件：写完了递归算法, 运行的时候，经常会遇到栈溢出的错误，就是没写终止条件或者终止条件写的不对，操作系统也是用一个栈的结构来保存每一层递归的信息，如果递归没有终止，操作系统的内存栈必然就会溢出。
  3. 确定单层递归的逻辑：确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
js
// 以前序遍历为例
// 1
traversal(node,res)
// 2
if(!node) return;
// 3
res.push(node.res);
traversal(node.left)
traversal(node.right)

前序遍历

js
function preorderTraversal(root) {
    function traversal(nodejs, res) {
        if (!node) return;
        res.push(node.value);
        traversal(node.left, res);
        traversal(node.right, res);
    }
    const res = [];
    traversal(root, res);
    return res;
}

中序遍历

js
function inorderTraversal(root) {
    function traversal(nodejs, res) {
        if (!node) return;
        traversal(node.left, res);
        res.push(node.value);
        traversal(node.right, res);
    }
    const res = [];
    traversal(root, res);
    return res;
}

后序遍历

js
function postorderTraversal(root)[] {
    function traversal(nodejs, res) {
        if (!node) return;
        traversal(node.left, res);
        traversal(node.right, res);
        res.push(node.value);
    }
    const res = [];
    traversal(root, res);
    return res;
}

迭代遍历

前序遍历

js
function preorderTraversal(root)[] {
    const res= [];
    if(!root) return [];
    const stack = [];
    stack.push(root);
    while(stack.length) {
        const cur = stack.pop();
        res.push(cur.val);
        cur.right && stack.push(cur.right);
        cur.left && stack.push(cur.left);
    }
    return res;
}

后序遍历

js
function postorderTraversal(root)[] {
    const res= [];
    if(!root) return [];
    const stack = [];
    stack.push(root);
    while(stack.length) {
        const cur = stack.pop();
        res.push(cur.val); // 前
        cur.left && stack.push(cur.left);
        cur.right && stack.push(cur.right);
    }
    return res.reverse();
}

中序遍历

js
function inorderTraversal (root) {
    const res = [];
    if (!root) return res;
    const stack = [];
    let cur = root;
    while (cur || stack.length) {
        if (cur) {
            stack.push(cur);
            cur = cur.left
        } else {
            cur = stack.pop();
            res.push(cur.val);
            cur = cur.right;
        }
    }
    return res;
}

真题演练

前序、中序、后序、层序遍历不再单独列出

翻转二叉树

leetcode 226

层序遍历

js
function invertTree(root) {
    if (!root) return root;
    let stack = [root];
    while (stack.length) {
        const cur = stack.pop();
        const [left, right] = [cur.left, cur.right];
        cur.left = right;
        cur.right = left;
        cur.left && stack.push(cur.left);
        cur.right && stack.push(cur.right);
    }
    return root;
};

Copyright © 2022-2023 ermuz